Codeforces Round 984 (Div. 3) F. (XORificator 3000)题解

https://codeforces.com/problemset/problem/2036/F

当我看到这道题的时候我就感觉很熟悉，不过调了1个多小时能做出来还是挺高兴的。

题意

那这道题该怎么做呢？我们可以从异或的性质入手，我们可以发现1-n的异或和满足一个性质：

同理对于对于不满足的那些数也同样满足类似的性质：

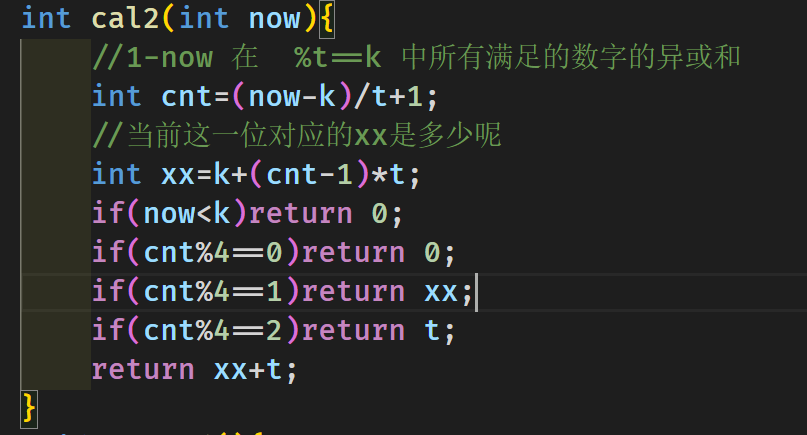
那么就可以用前缀异或的思想求区间异或和，答案就迎刃而解了。

//#pragma GCC optimize("Ofast")
//#pragma GCC optimize("Ofast,no-stack-protector,unroll-loops,fast-math")
//#pragma GCC target("sse,sse2,sse3,ssse3,sse4.1,sse4.2,avx,avx2,popcnt,tune=native")
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define double long double
const int N=2e5+7;
int t;
int l,r,x,k;
int cal(int x){
    if(x%4==0)return x;
    if(x%4==1)return 1;
    if(x%4==2)return x+1;
    return 0;
}
int cal2(int now){
    //1-now 在  %t==k 中所有满足的数字的异或和
    int cnt=(now-k)/t+1;
    //当前这一位对应的xx是多少呢
    int xx=k+(cnt-1)*t;   
    if(now<k)return 0;
    if(cnt%4==0)return 0;
    if(cnt%4==1)return xx;
    if(cnt%4==2)return t;
    return xx+t;
}
void solved(){
    cin>>l>>r>>x>>k;
    int ans1=cal(r)^cal(l-1);
    t=(1ll<<x);
    int ans2=cal2(r)^cal2(l-1);
    cout<<(ans1^ans2)<<'\n';
}

signed main(){
    auto begin = std::chrono::high_resolution_clock::now();
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int _=1;
    cin>>_;
    while(_--)solved();
    auto end = std::chrono::high_resolution_clock::now();
    auto elapsed = std::chrono::duration_cast<std::chrono::nanoseconds>(end - begin);
    //cerr << "Time measured: " << elapsed.count() * 1e-9 << " seconds."; 
    return 0;
}